Time Complexity Analysis with Big O Notation

Big O is a type of Asymptotic notation (the other two are: Big Omega and Big Theta). In Math, Asymptotic notations allow you to describe the rate of growth of a function. In Computer Science, Big O is used to describe the performance of an algorithm in terms of the number of operations that need to be executed as the input size grows in the worse case.
Formal Definition of Big O
The formal definition of Big O is:
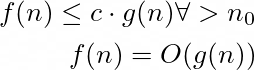
where:
- c is a constant >0

What does this mean? Let's break it down.
Suppose we have two functions:
- f(n)
- g(n)
We are going to compare these two functions on the basis of their rate of growth. For this we are going to use Big O notation. Let's graph both f(n) and g(n). This is what we get:
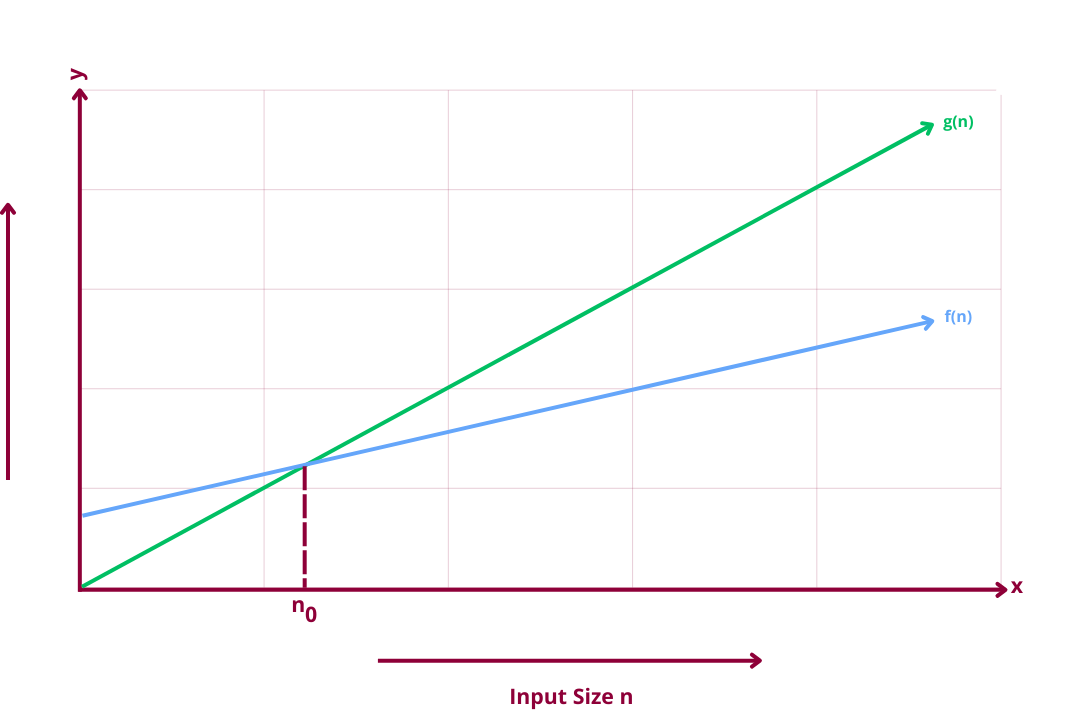
Big O notation says that for any point after n0 the function f(n) will always be ≤ g(n) for larger values approaching ∞. If this condition holds true then we say that f(n)=o(g(n)). Before n0 though the values of both functions can fluctuate.
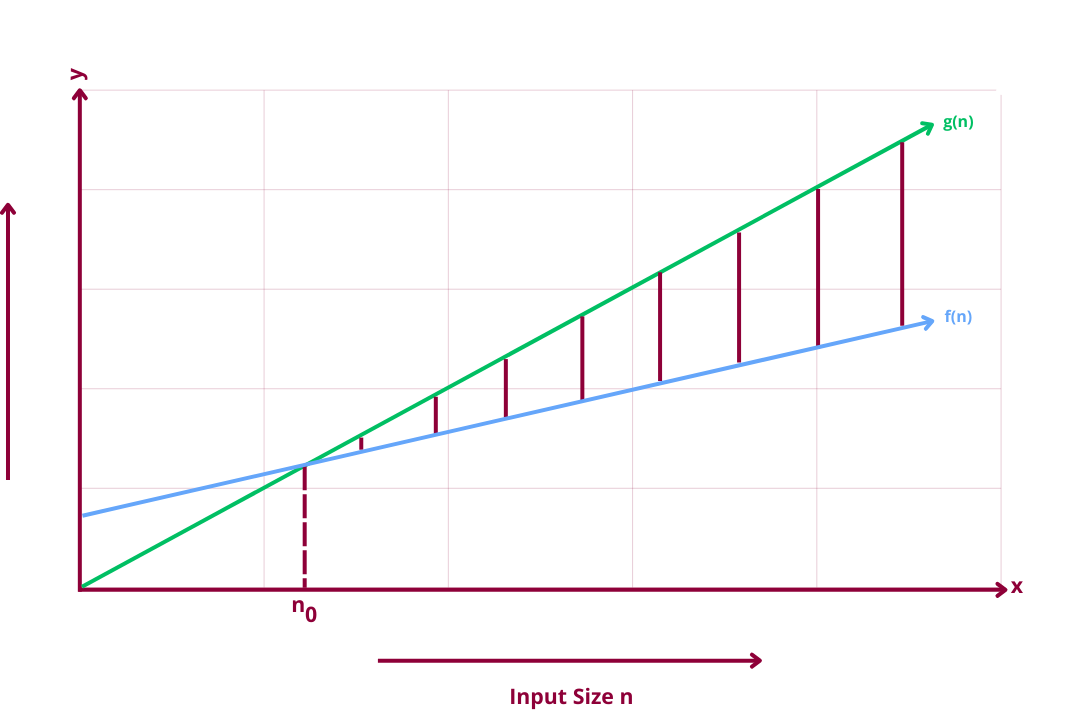
Let's go through some worked examples.
Worked Examples
Example 1
Suppose:
- f(n)=10n+200
- g(n)=n3
- Let c=1
| n | f(n) | g(n) |
| 1 | (10*1)+200=210 | 1*(1^3)=1 |
| 2 | 220 | 8 |
| 3 | 230 | 27 |
| 4 | 240 | 64 |
| 5 | 250 | 125 |
| 6 | 260 | 216 |
| 7 | 270 | 343 |
| 8 | 280 | 512 |
| 9 | 290 | 729 |
| 10 | 300 | 1000 |
| 11 | 310 | 1331 |
| 12 | 320 | 1728 |
| 13 | 330 | 2197 |
| 14 | 340 | 2744 |
| 15 | 350 | 3375 |
| 16 | 360 | 4096 |
| 17 | 370 | 4913 |
| 18 | 380 | 5832 |
| 19 | 390 | 6859 |
| 20 | 400 | 8000 |
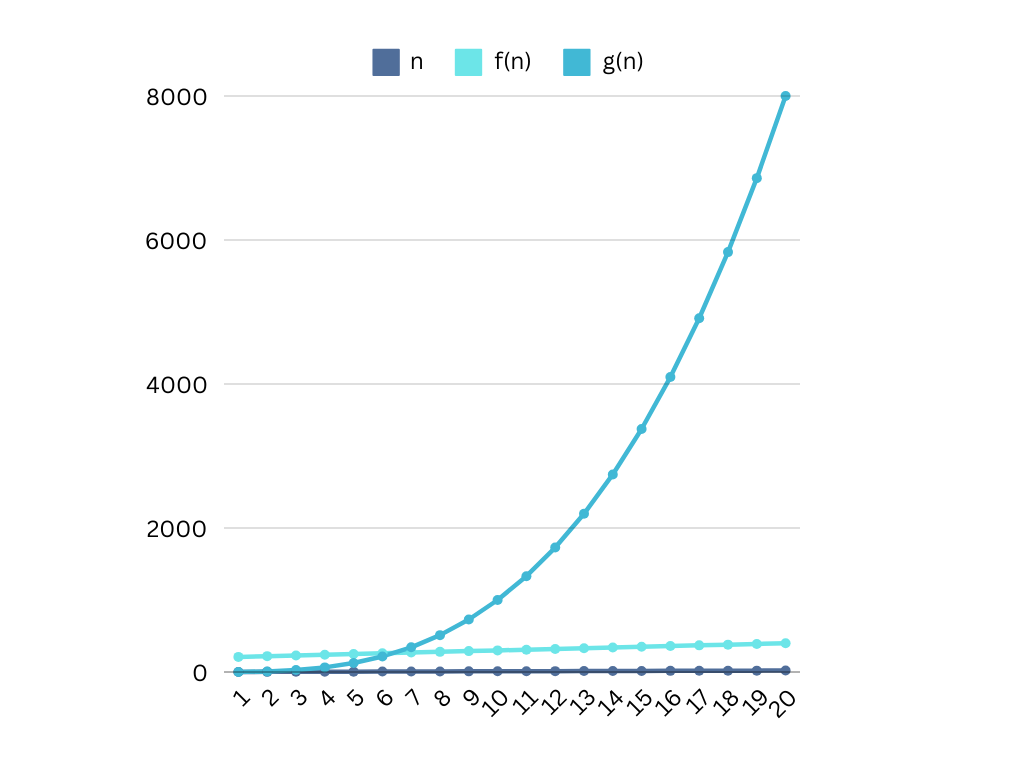
f(n)=o(g(n)) since for larger values approaching ∞ f(n) ≤ g(n).
Example 2
Suppose:
- f(n)=10n+200+n3
- g(n)=n3
- Let c=1
| n | f(n) | g(n) |
| 1 | (10*1)+200+(1^3)=211 | 1*(1^3)=1 |
| 2 | 228 | 8 |
| 3 | 257 | 27 |
| 4 | 304 | 64 |
| 5 | 375 | 125 |
| 6 | 476 | 216 |
| 7 | 613 | 343 |
| 8 | 792 | 512 |
| 9 | 1019 | 729 |
| 10 | 1300 | 1000 |
| 11 | 1641 | 1331 |
| 12 | 2048 | 1728 |
| 13 | 2527 | 2197 |
| 14 | 3084 | 2744 |
| 15 | 3725 | 3375 |
| 16 | 4456 | 4096 |
| 17 | 5283 | 4913 |
| 18 | 6212 | 5832 |
| 19 | 7249 | 6859 |
| 20 | 8400 | 8000 |
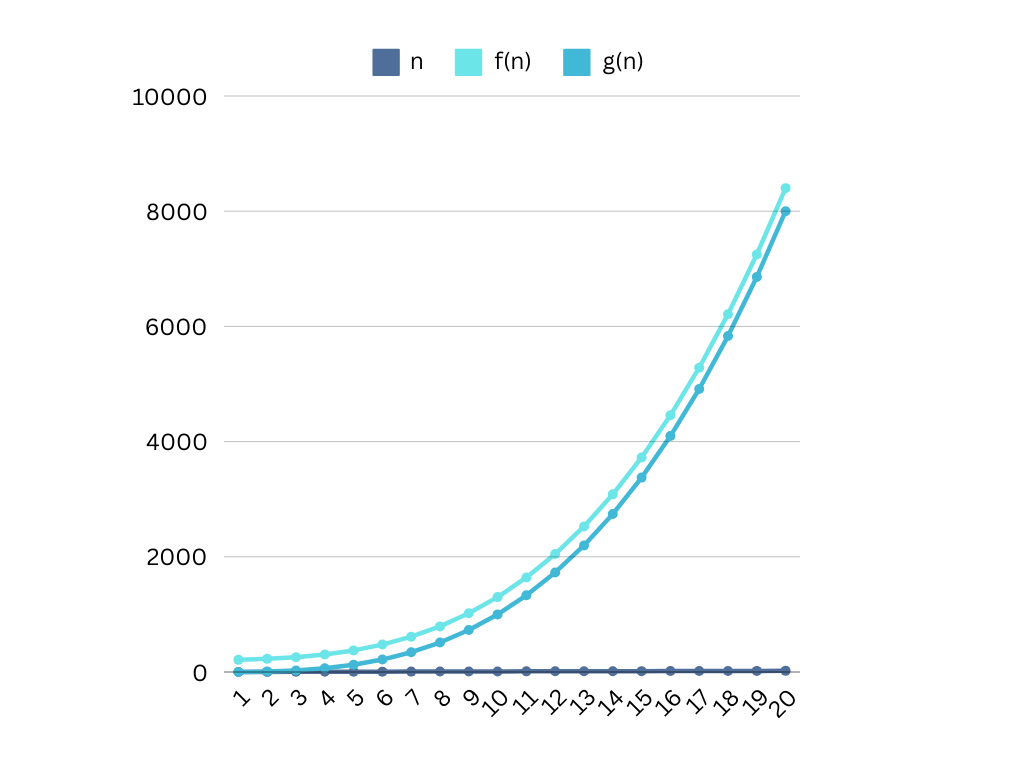
f(n) is not o(g(n)) since for larger values approaching ∞ g(n) ≤ f(n).
Example 3
Suppose:
- f(n)=10n+200+n3
- g(n)=n3
- Let c=10
| n | f(n) | g(n) |
| 1 | (10*1)+200+(1^3)=211 | 10*(1^3)=10 |
| 2 | 228 | 80 |
| 3 | 257 | 270 |
| 4 | 304 | 640 |
| 5 | 375 | 1250 |
| 6 | 476 | 2160 |
| 7 | 613 | 3430 |
| 8 | 792 | 5120 |
| 9 | 1019 | 7290 |
| 10 | 1300 | 10000 |
| 11 | 1641 | 13310 |
| 12 | 2048 | 17280 |
| 13 | 2527 | 21970 |
| 14 | 3084 | 27440 |
| 15 | 3725 | 33750 |
| 16 | 4456 | 40960 |
| 17 | 5283 | 49130 |
| 18 | 6212 | 58320 |
| 19 | 7249 | 68590 |
| 20 | 8400 | 80000 |
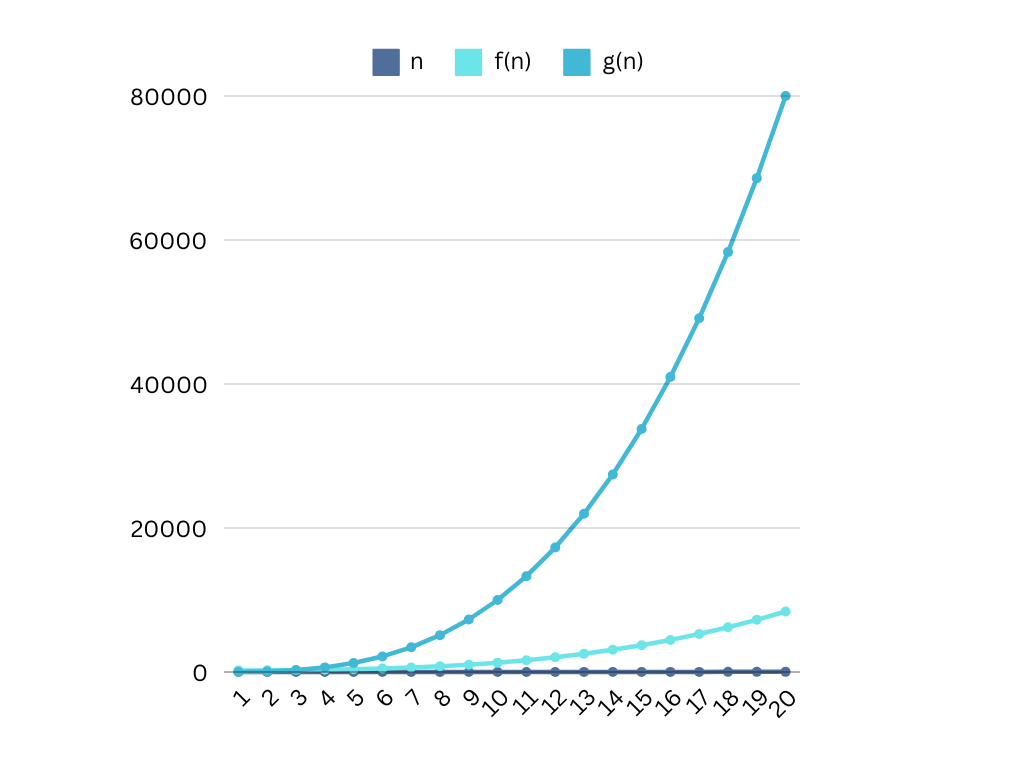
f(n)=o(g(n)) since for larger values approaching ∞ f(n) ≤ g(n) where c=10.