Cost Function in Linear Regression

A cost function is nothing but a measurement of how good or bad a model is performing. It does this by measuring the difference between the predicted values of the model and the actual values of the training data. The lower the difference between predicted and actual values, the higher the accuracy of the model. The higher the difference between predicted and actual values, the lower the accuracy of the model. The goal is to minimize the difference between the predicted and actual values thereby enhancing model accuracy. A popular metric used to evaluate the performance of regression models is Mean Squared Error.
Introducing Mean Squared Error
The formula for Mean Squared Error is:
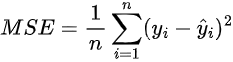
where:
- n is the number of items in the dataset
- yi is the actual value
- ŷi is the predicted value
Mean Squared Error calculates the average squared difference between the actual and predicted values. The reason for squaring the difference is such that if the predicted value is far from the actual value, then a penalty is applied.
Let's go through a worked example.
A Worked Example of Mean Squared Error
Let's assume we have the following dataset consisting of actual and predicted values for a regression problem.
Actual values = [ 26, 92, 65 ]
Predicted values = [ 25, 100, 55 ]
Let's calculate the Mean Squared Error.
Step 1 - Calculate the difference between all of the actual and predicted values
Differences = [ 1, -8, 10 ]
Step 2 - Square the differences
Squared differences = [ 1, 64, 100 ]
Step 3 - Find the Mean Squared Error
Mean Squared Error = (1/3) * (1 + 64 + 100) = 55
Therefore the Mean Squared Error for this model is 55.
Limitations of Mean Squared Error
While Mean Squared Error (MSE) is a valuable metric, it is not robust to outliers. Outliers are data points that are significantly distant from the other data points. MSE penalizes significant deviations caused by outliers. A single data point with a significant difference between the actual and predicted value can amplify the MSE score. This can be misleading and may not truly reflect model performance.