Detecting Outliers using the Interquartile Range (IQR)

Outliers are data points that are significantly distant from the other data points. Outliers in Machine Learning can be either useful or not so useful. Suppose a bank has a dataset which contains credit card transactions for a particular customer. In this case, the outliers in the dataset can be used to identify fraudulent transactions. But if outliers exist due to human error, then it is not so useful because outliers in the dataset are not genuine outliers - they are just errors.

How do we go about finding outliers in a dataset?

We can use the IQR to find outliers in a dataset. This is a just a measure of where the bulk of the values lie in the dataset and from that we can detect outliers.

Let's go through a worked example.

A Worked Example of IQR

Let's assume we have the following dataset:

[ 81, 61, 34, 26, 92, 65, 76, 89, 63, 61, 97 ]

This data could represent anything. This could be the number of times a particular movie has been watched. For example, the movie Star Wars: Episode V - The Empire Strikes Back has been watched 97 times. While, the movie Alien has only been watched 26 times.

Let's find out the IQR of the dataset. There are a few steps that we need to follow in order to get to the IQR.

Step 1 - Arrange the data in ascending order

The data arranged in ascending order:

[ 26, 34, 61, 61, 63, 65, 76, 81, 89, 92, 97 ]

Step 2 - Find the Median value in the dataset

The median is the middle value of the dataset. In this case the middle value is 65.

[ 26, 34, 61, 61, 63, 65, 76, 81, 89, 92, 97 ]

Step 3 - Find Quartile 1 (Q1) value in the dataset

This involves finding the middle value (median) of the first half of the dataset (excluding the median 65) which is 61.

[ 26, 34, 61, 61, 63, 65, 76, 81, 89, 92, 97 ]

Step 4 - Find Quartile 3 (Q3) value in the dataset

This involves finding the middle value (median) of the last half of the dataset (excluding the median 65) which is 89.

[ 26, 34, 61, 61, 63, 65, 76, 81, 89, 92, 97 ]

Step 5 - Find IQR of the dataset

Finally, we can calculate the IQR of the dataset. This involves simply calculating the difference between Q1 and Q3.

Q1 = 61

Q3 = 89

IQR = 89 - 61 = 28

Box Plots

We can represent the IQR as a box plot. This shows the distribution of data and can be used for exploratory data analysis.

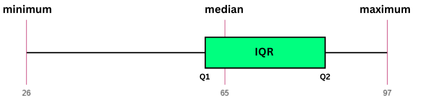
It displays a five number summary including:

• Minimum - the smallest value in the dataset (26)
• First quartile - the Q1 value in the dataset (61)
• Median - the middle value of the dataset (65)
• Third quartile - the Q3 value in the dataset (89)
• Maximum - the largest value in the dataset (97)

Detecting Outliers

To detect outliers, we can define lower and upper bounds to the dataset. Any data that falls outside of the lower and upper bounds is categorized as an outlier.

To define the lower bound, we use the formula:

Q1 - 1.5(IQR)

For the purposes of the example dataset, the lower bound is:

61 - 1.5(28) = 19

To define the upper bound, we use the formula:

Q3 + 1.5(IQR)

For the purposes of the example dataset, the upper bound is:

89 + 1.5(28) = 131

The upper and lower bounds give a range of [19, 131]. This means that any data point that is not within this range, will be categorized as an outlier. Looking at the dataset:

[ 26, 34, 61, 61, 63, 65, 76, 81, 89, 92, 97 ]

We can see that all data points fall within the [19, 131] range. If there was some data point that was outside of this range (e.g. the data point 207), then this would be categorized as an outlier.