Term Frequency-Inverse Document Frequency

Term Frequency-Inverse Document Frequency (TF-IDF) is a measure of:
- How many times a given term appears in a document - Term Frequency
- How many times the same term appears in other documents (corpus) - Inverse Document Frequency
TF-IDF is used to quantify how relevant a given term is within a document relative to a corpus. TDF-IDF is used in Information Retrieval (e.g. Search Engines) and Machine Learning.
Understanding the Math behind TF-IDF
Let's first understand the math used to determine TF, IDF and then TF-IDF.
Term Frequency
TF is a measure of the number of times a given term appears in a document. The formula for TF is:
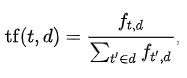
where:
- ft,d is the number of times a term t appears in a document d
- divided by the sum of all of the terms found in that document
A simpler way of writing this formula is:

Inverse Document Frequency
IDF is a measure of the number of times the same term appears in other documents (corpus). The formula for IDF is:
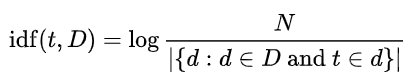
where:
- N is the total number of documents in a corpus D
- divided by the number of documents where the term t appears
A simpler way of writing this formula is:

Term Frequency-Inverse Document Frequency
Using the TF and IDF quantities, we can now calculate the TF-IDF. The formula for TF-IDF is:
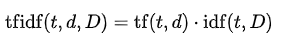
where:
- TF is multiplied with IDF to get the TF-IDF score
A Worked Example
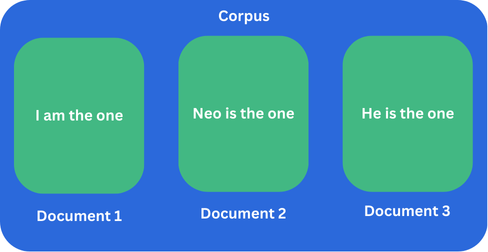
Let's go through a worked example of how TF-IDF is calculated. In this example, there is a Corpus with 3 documents each containing some text.
- Document 1 contains the text "I am the one"
- Document 2 contains the text "Neo is the one"
- Document 3 contains the text "He is the one"
Let's first list out how many times each term appears in each document.
| Term | Frequency |
|---|---|
| I | 1 |
| am | 1 |
| the | 3 |
| one | 3 |
| Neo | 1 |
| is | 2 |
| He | 1 |
Term Frequency
Now let's calculate the TF i.e. the number of times a given term appears in a document
| Term | Document 1 | Document 2 | Document 3 |
|---|---|---|---|
| I | 1/4=0.25 | 0 | 0 |
| am | 1/4=0.25 | 0 | 0 |
| the | 1/4=0.25 | 1/4=0.25 | 1/4=0.25 |
| one | 1/4=0.25 | 1/4=0.25 | 1/4=0.25 |
| Neo | 0 | 1/4=0.25 | 0 |
| is | 0 | 1/4=0.25 | 1/4=0.25 |
| He | 0 | 0 | 1/4=0.25 |
Inverse Document Frequency
Now let's calculate the IDF i.e. the number of times the same term appears in other documents.
| Term | Document 1 | Document 2 | Document 3 |
|---|---|---|---|
| I | log(3/1)=0.47 | 0 | 0 |
| am | log(3/1)=0.47 | 0 | 0 |
| the | log(3/3)=0 | log(3/3)=0 | log(3/3)=0 |
| one | log(3/3)=0 | log(3/3)=0 | log(3/3)=0 |
| Neo | 0 | log(3/1)=0.47 | 0 |
| is | 0 | log(3/2)=0.17 | log(3/2)=0.17 |
| He | 0 | 0 | log(3/1)=0.47 |
Term Frequency-Inverse Document Frequency
Finally let's calculate the TF-IDF i.e. multiplying the TF with IDF to get the TF-IDF score.
| Term | Document 1 | Document 2 | Document 3 |
|---|---|---|---|
| I | 0.25*0.47=0.11 | 0 | 0 |
| am | 0.25*0.47=0.11 | 0 | 0 |
| the | 0.25*0=0 | 0.25*0=0 | 0.25*0=0 |
| one | 0.25*0=0 | 0.25*0=0 | 0.25*0=0 |
| Neo | 0 | 0.25*0.47=0.11 | 0 |
| is | 0 | 0.25*0.17=0.04 | 0.25*0.17=0.04 |
| He | 0 | 0 | 0.25*0.47=0.11 |
The higher the TF-IDF score the more relevant the term is. As the term gets less relevant, the score will approach 0. In other words, if a term appears multiple times in a document, the importance score increases (TF). But if the same term appears many times in other documents then it may just be a common term and hence has no relevance so the importance score decreases (IDF). TF-IDF is a balance between TF and the rarity of the term in other documents in the corpus.
The terms the and one are given a score of 0 because these terms are less relevant. However, the terms I, am, Neo, is and He are given higher scores and hence are more relevant.