Understanding Cosine Similarity

Cosine similarity is used to measure how similar things are. Mathematically, it's a measure of similarity between two or more vectors. Cosine similarity is widely used in Machine Learning and Data Science, particularly when measuring similarity between vectors projected in a multidimensional space.
The formula for Cosine similarity for two vectors A and B is:
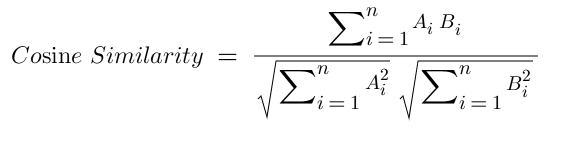
Let's go through a worked example.
Worked Example of Calculating Cosine Similarity
Let's assume we have the following vectors A and B:
A = [ 2, 7, 9, 12 ]
B = [ 1, 3, 16, 21 ]
Step 1 - Calculate the dot product of Vectors A and B
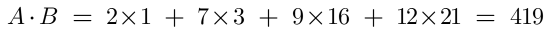
Step 2 - Calculate the magnitude of Vectors A and B
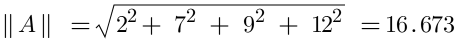
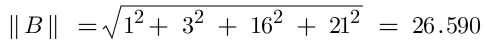
Step 3 - Calculate the Cosine similarity
The cosine can be calculated by dividing the dot product by the magnitude.
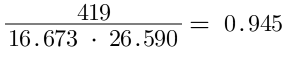
The cosine similarity is 0.945. We can use the cosine similarity to find the angle between vectors A and B by applying the arccosine function and represent this on a 2-dimensional graph. Smaller angles indicate higher similarity.
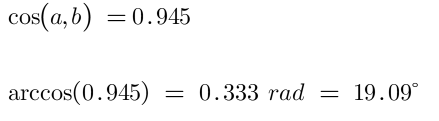

Calculating Cosine Similarity in R
The lsa package in R provides a cosine function that can be used to calculate the cosine similarity between vectors in R.
library(lsa)
# Define vectors a and b
a <- c(2, 7, 9, 12)
b <- c(1, 3, 16, 21)
# Calculate cosine similarity and display results
print(cosine(a, b))